“斐波那契数列”的读音是什么？斐波那契比例如何使用

文章目录

“斐波那契数列”的读音是什么？

“斐波那契数列”的读音是fěi bō nà qì shù liè

拼音：fěi bō nà qì shù liè

别 称：

黄金分割数列、兔子数列

提出者：

意大利数学家 列昂纳多·斐波那契，生于公元1170年，卒于1250年，籍贯是 比萨。他被人称作“比萨的 列昂纳多”。

九年级黄金比例知识点？

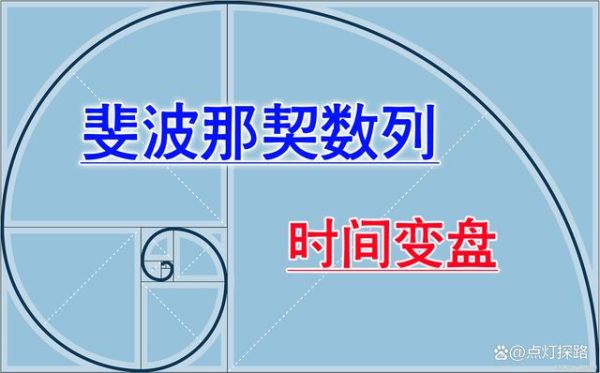
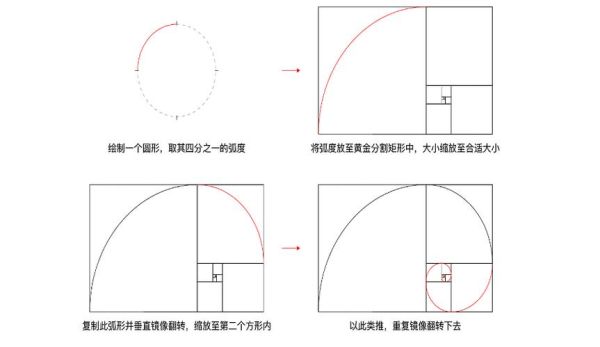
黄金分割点比例计算公式是：(√5-1)/2。

黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数，取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽，因此称为黄金分割，也称为中外比。

通常用Φ表示。这是一个十分有趣的数字，以0.618来近似表示，通过简单的计算就可以发现：(1-0.618)/0.618≈0.618，即一条线段上有两个黄金分割点。

黄金比例是一个数学概念，也被称为黄金分割或黄金比例。它指的是将一条线段分成两个部分，在两部分的长度比例上，较长部分与整体的长度之比等于较短部分与较长部分的长度之比。

以下是九年级黄金比例的相关知识点：

定义：黄金比例可以用符号 φ 表示，其值约等于 1.6180339887，也可以用符号 Φ 表示其倒数即 0.6180339887。根据定义，a/b = (a+b)/a = φ。

出现形式：

在艺术和建筑中，黄金比例被广泛应用于设计，例如画作的构图、建筑物的比例、雕塑的比例等。

在自然界中，一些生物体的身体结构或器官比例也符合黄金比例，例如素描中的人体比例、花朵的排列方式等。

黄金矩形：黄金比例还与矩形相关。黄金矩形是一个长宽比接近黄金比例的矩形，即长边长度与短边长度之比约等于 φ。

数学性质：

φ 的平方等于 φ+1，即 φ^2 = φ+1。

φ 和 Φ 互为倒数，即 φ×Φ = 1。

设整条线段为 1 ,
则较长的线段=(√5-1)/2≈0.618 ,
较短的线段=1-(√5-1)/2=(3-√5)/2≈0.382 .
∴ 短的比长的=[(√5-1)/2]/1=(√5-1)/2≈0.618 ,
∴ 长的比短的=1/[(√5-1)/2]=(√5+1)/2≈1.618 .
∴ 短的线段比整条线段=[(3-√5)/2]/1=(3-√5)/2≈0.382 .
∴ 3减根号5/2就是“短的线段比整条线段”.

斐波那契时区？

股票和基金领域，斐波那契时区是一组垂直线，代表可能出现高点、低点或反转的潜在时间区域。用斐波那契时区可以找到股票和基金发生反转的潜在时间区域。

斐波那契时区是基于时间的技术分析。 该指标通常从图表上的主要摆动高点或摆动低点开始。 然后几条垂直线向右延伸，指示可能导致另一个显着摆动高点、摆动低点或反转点的时间区域。 这些垂直线对应于价格图表上的时间轴，按斐波那契数列的比例来划分。

到此，以上就是小编对于斐波那契比率怎么用的问题就介绍到这了，希望介绍的3点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。